How to Build (and Understand) a Neural Network Pt. 1: The Perceptron
December 30, 2016
Building a neural network is fairly easy. It doesn’t require you to know any obscure programming language, and you can build a working model with surprisingly few lines of code. To understand how it works however — to really understand it — takes mathematical insight more than anything else. While this may sound lofty, anyone with a firm grasp of high school level math is equipped to take on the task.
This is the first in a series of posts that will culminate in us building a neural network in Python. It will be a rudimentary one, but at the end, we will have covered all of the concepts that make it tick. Hopefully, this will set us both on a path to deepen our knowledge of how to make machines smart.
A good place for us to start is the perceptron algorithm. According to Wikipedia:
The perceptron algorithm dates back to the late 1950s; its first implementation, in custom hardware, was one of the first artificial neural networks to be produced.
Perceptrons are a good place to start because they showcase the power and versatility of learning algorithms while remaining very simple. Once we are comfortable with perceptrons, we can use this as a springboard to tackle some of the more sophisticated concepts in machine learning.
We’ll start off with some overall theory, followed by an introduction to the actual algorithm. Finally, we’ll code a working perceptron in Python.
Overall theory
The perceptron algorithm is a binary classification algorithm, which is to say that it can tell whether a piece of data belongs to one of two classes. To get a better sense of what this means, let’s take a look at the following plot:
This is a scatter plot of part of the Iris dataset; the de facto dataset for training a perceptron. The full dataset contains 150 samples of three different types of Iris flower (50 samples of each type). Each sample contains four features: sepal width, sepal length, petal width, and petal length. In the scatter plot above, we are only looking at two features (petal width and petal length) for two types of Iris (setosa and versicolor).
The thing to notice about the data is that it is linearly separable. In other words, the points belonging to each Iris type are clustered in such a way that you can separate them with a straight line. What the perceptron algorithm does is it automatically ‘learns’ the parameters for a model (in this case a linear function) that, when presented with the features of a sample, returns a positive number for one Iris type, and a negative number for the other. This enables us to classify a sample as belonging to the setosa family or the versicolor family solely by looking at the features of the flower.
The following steps outline how to create a model with this capability.
- We initialize a number of parameters with random values between 0 and 1. If each of our samples has $n$ features, we initialize $n+1$ parameters. Out of these $n+1$ parameters, there will be $n$ weights, and one so-called bias. There will always be an equal number of weights and features. I will get to the point of the parameters in a minute, but for the moment, you can think of them as the knobs and dials of our model, which our algorithm uses to improve its performance.
- Having initialized our parameters, we now feed training data to our (currently random, and thus highly inaccurate) model one sample at a time. The model takes the features of a sample as input, and multiplies each feature by the model’s corresponding weight. This yields our weighted features.
- Next, we calculate the sum of the weighted features and add the bias. At this point, all we are left with is a number. If this number is less than zero, we classify the sample as belonging to the setosa family; if the number is greater than zero, we classify the sample as being of type versicolor.
- Last but not least, if our prediction is wrong, we update our parameters. If our prediction is right, we do nothing, and move on to the next sample.
This last step tells us that what we are dealing with here is supervised learning. The reason it is “supervised” is that we already know the right answer — aka. the “label” — for every sample. The label will either be 0 or 1, respectively representing setosa and versicolor. Knowing the right answer lets us adjust the parameters of our model every time it performs poorly. That way, looping over each sample will incrementally improve its accuracy.
The math
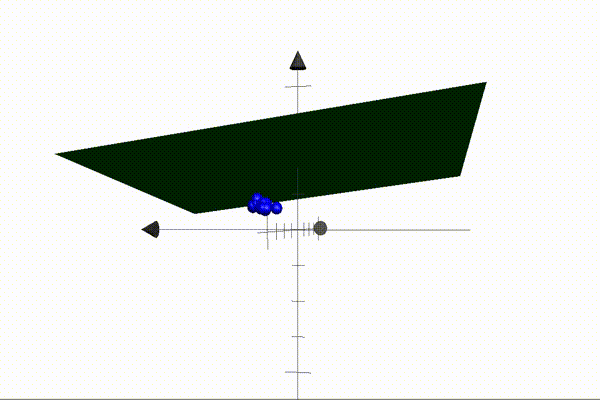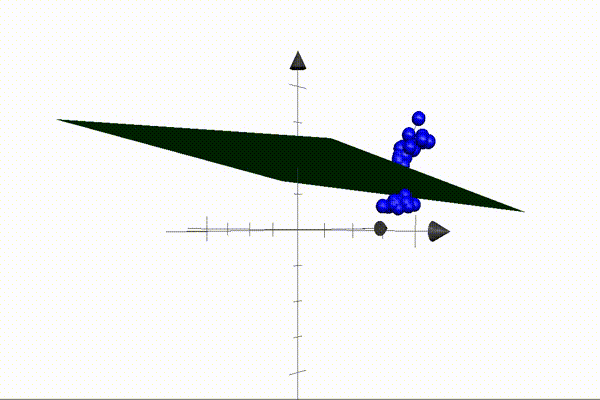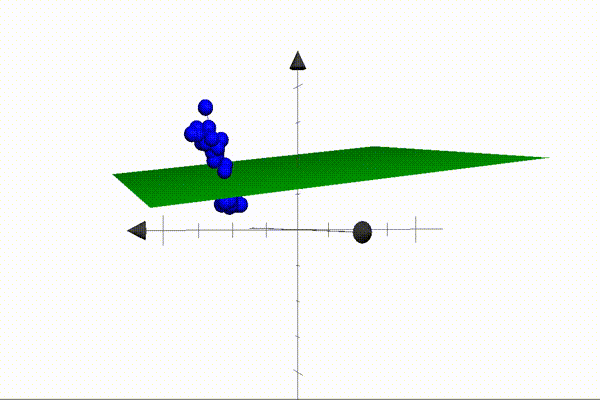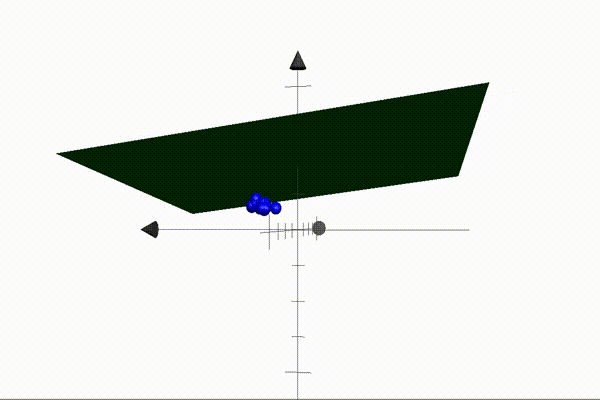
The animation above illustrates an example of a 2D plane separating setosa and versicolor points in 3D space. Our parameters define the plane — also known as the decision boundary — and when these are multiplied by the coordinates of a point (the features), the result will be positive if the point is located above the plane, and negative when located below the plane. This is the core idea that makes our algorithm possible. Our job is to find a set of parameters that separate the classes perfectly (like the one above).
The four features of every sample will be represented by a four-dimensional vector $x$. The vector $\theta$ will be a four-dimensional vector containing the weights. If $b$ is the bias, we can mathematically represent our model like this:
€€ \theta_1x_1 + \theta_2x_2 + \theta_3x_3 + \theta_4x_4 + b €€
With four coordinates ($x_1$ to $x_4$), this expression defines a cube in 4D space rather than a plane in 3D space like the one shown in the animation. Impossible to visualize, yes, but that doesn’t change a thing. Pretty cool, right?
A brief note about terminology: We can refer to a line in 2D space, a plane in 3D space, a cube in 4D space, and so on by the same name: hyperplane. More generally, a hyperplane is simply a space of dimension $n-1$ in an enclosing space of dimension $n$. As we will see, this will be a convenient term as we expand our algorithms to higher dimensions.
It is worth repeating that – for 3D space – when this expression is positive, the point $x$ is located above the plane, and when the expression is negative, $x$ is located beneath the plane. The plane itself is defined by the parameters $\theta$ and $b$, where $\theta$ is responsible for “tilting” the plane, and $b$ either pushes or pulls the plane up or down in the coordinate space. Note that all of this holds true for higher dimensional hyperplanes as well.
Keep in mind that our weights and features are represented as vectors. This allows us to rewrite the above expression by taking the dot product of $x$ and $\theta$, and then adding $b$ to the resulting scalar:
€€ (x \cdot \theta) + b €€
To make things even more concise, we will add another element $x_0$ to our vector $x$ and make sure that it is always equal to 1. We will also add a corresponding weight $\theta_0$ to our vector $\theta$. This allows us to treat the bias (now represented as $\theta_0$) as part of our vector operations, so we can simplify the above expression even further:
€€ x \cdot \theta €€
Spelled out, this is now equal to:
€€ \begin{Bmatrix}1 \cr x_1 \cr x_2\cr x_3 \cr x_4 \end{Bmatrix} \cdot \begin{Bmatrix}\theta_0 \cr \theta_1 \cr \theta_2 \cr \theta_3 \cr \theta_4\end{Bmatrix} = \theta_0 + \theta_1x_1 + \cdots + \theta_4x_4 €€
All of this may seem like mere mathematical housekeeping, but as we will see, it will keep our code neat and tidy, and — much more importantly — it will allow us to vectorize our computations. Vectorization is important, since it enables significant computational speedups, as soon as we begin to handle more complex models with larger amounts of data. (For a small dataset like ours, it won’t really make a difference, but it is good practice to keep it in mind.)
We will now define a function known as the heaviside step function or unit step function:
€€ \sigma(z)=\begin{cases} 1 & {\small z > 0,} \cr 0 & \text{otherwise} \end{cases} €€
If it isn’t immediately obvious from this definition, the heaviside step function takes a scalar input $z$ and returns 1 if $z$ is positive, and 0 if $z$ is nonpositive. The sole purpose of the heaviside step function is to classify points below the decision boundary as 0, and points above the decision boundary as 1. The output will thus be our prediction of the Iris type.
For each sample, the output $\hat{y}$ of our model will be:
€€ \hat{y} = \sigma(x \cdot \theta) €€
Now to the most important part. In order for the network to ‘learn’ a function — which is to say a bias and a set of weights — that produces a plane which separates setosa and versicolor points, we will need a learning algorithm. Fortunately, the perceptron learning algorithm is super simple:
€€ \Delta \theta_i = (y^{(j)} - \hat{y}^{(j)})x_i^{(j)} €€
$j$ represents the $j$th sample, and $i$ represents the $i$th feature. $y^{(j)}$ is the true label.
If you are not used to mathematical notation, this may seem a little intimidating. Not to worry; it is easy to see what is happening here by looking at an example.
Let’s assume that, during training, the model erroneously interprets setosa features for versicolor features. The heaviside step function would then output a 1 when it should have given us a 0. In this case, $\Delta \theta_i$ would be:
€€ \Delta \theta_i = (0 - 1)x_i^{(j)} €€
If $x_i^{(j)}$ were, say, the petal length of our misclassified sample with a value of 1.9, the equation would look like this:
€€ \Delta \theta_i = (-1) \cdot 1.9 = -1.9 €€
We would then subtract 1.9 from $\theta_i$’s current value.
To see why we subtract, remember that the output of the model was 1 when it should have been 0. This means that the result of the dot product $(x \cdot \theta)$ was positive when it should have been negative, and therefore that the parameters are currently adjusted too high. Had we predicted a 0 when the true label was 1, the value of $\theta_i$ would have been increased by 1.9.
This same learning algorithm holds for the bias. However, since the bias’ corresponding “feature” is 1, this leaves us with:
€€ \Delta \theta_0 = (y^{(j)} - \hat{y}^{(j)}) €€
And that’s it!
A cool thing about the perceptron algorithm is that it is guaranteed to find exactly the right parameters that separate the two classes at 100% accuracy (granted that the data is linearly separable of course). The question is whether these parameters generalize and enable the model to correctly predict the classes of samples that weren’t in the training set.
Getting our hands dirty
To start off, make sure that you have Python and NumPy installed on your machine. If you are not already familiar with NumPy, it is an essential package for Python for doing matrix and vector operations. There will be tons of these going forward.
To import and handle the Iris dataset, we will use Pandas. NumPy as well as Pandas can be installed by running pip3 install numpy and pip3 install pandas in the command line. Once you’ve got everything set up, we’ll create a new Python file and do the requisite imports at the top. We will also be including the Iris dataset made available from UCI’s website. As a courtesy, you may want to download the file and reference it locally in order to spare UCI of unnecessary traffic.
import numpy as np
import pandas as pd
dataset = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data")
# Combining half the setosa features and half the versicolor features into our training dataset
train_features = np.append(dataset.iloc[0:25, 0:4].values, dataset.iloc[50:75, 0:4].values, axis=0)
train_targets = np.append(dataset.iloc[0:25, 4].values, dataset.iloc[50:75, 4].values, axis=0)
# Combining the remaining setosa and versicolor features into the test dataset
test_features = np.append(dataset.iloc[25:50, 0:4].values, dataset.iloc[75:100, 0:4].values, axis=0)
test_targets = np.append(dataset.iloc[25:50, 4].values, dataset.iloc[75:100, 4].values, axis=0)
# Appending 1 as the first feature of each sample, so theta0 can act as the bias
train_features = np.c_[np.ones((train_targets.shape[0], 1)), train_features]
test_features = np.c_[np.ones((test_targets.shape[0], 1)), test_features]
# Changing the name of the two flower types into our target values 0 and 1
train_targets = np.where(train_targets == "Iris-setosa", 0, 1)
test_targets = np.where(test_targets == "Iris-setosa", 0, 1)
# Converting the target arrays from 50x1 matrices to 50D vectors
train_targets = train_targets.reshape((50))
test_targets = test_targets.reshape((50))I hope the comments make it clear what is going on here.
We will use the training samples to train the model, and our test samples to verify whether the model generalizes and correctly predicts the classes of unseen samples. A 50/50 split between training and test samples is not very common (usually it is 60/40 or 70/30 with the majority going to the training samples), but it should suffice for this example.
Note that all training samples are now stored within a 50x5 matrix $X$. If you are unfamiliar with matrices, they can simply be thought of as containers of multiple vectors. Thus, the 50x5 matrix contains 50 samples/vectors, and each of those vectors contains four features and a bias. In other words, our matrix $X$ contains 50 $x$s.
Now that we have our data organized and ready, it is time to code the actual perceptron. Let’s start by creating a Perceptron class with a fit method that takes three parameters: X, y and epochs. X will be our matrix of features, y will be a vector containing the corresponding target values, and epochs will be an integer specifying how many times to loop over the training data. If we didn’t specify the number of epochs, we would only have 50 iterations to update our parameters, which probably wouldn’t be enough for them to converge on the most optimal values.
class Perceptron(object):
def __init__(self):
super(Perceptron, self).__init__()
self.theta = np.random.rand(5)
def fit(self, X, y, epochs):
for _ in range(epochs):
for i in range(len(X)):
weighted_input = np.dot(X[i], self.theta)
y_hat = self.heaviside_step(weighted_input)
self.theta += np.multiply((y[i] - y_hat), X[i])
def heaviside_step(self, weighted_input):
return np.where(weighted_input >= 0, 1, 0)Believe it or not, this is the whole perceptron algorithm!
We start by initializing five random weights between 0 and 1. Then, the fit method loops over all samples epochs number of times. In the inner-most loop, we take the dot product between every feature vector X[i] and the parameter vector self.theta. The result of the dot product is handed over to the heaviside step function yielding our y_hat, and the parameters are then updated.
To benchmark how well our model performs, we will add a predict method to our class that uses the learned parameters self.theta to predict the classes of our test samples:
def predict(self, X):
weighted_input = np.dot(X, self.theta)
return self.heaviside_step(weighted_input)All there is left to do is feed some data to a Perceptron object:
# Initializing a Perceptron object and feeding it our training data
pcpt = Perceptron()
pcpt.fit(train_features, train_targets, 3)
# The model has now been trained. Time to benchmark!
est = pcpt.predict(test_features)
err = est - test_targets
err = np.where(err != 0, 1, 0)
acc = float((len(test_targets) - np.sum(err)) / len(test_targets))
print("Accuracy: %f" % acc)When running the script, you should see the following output:
$ python perceptron.py
Accuracy: 1.000000Because the data is linearly separable, the algorithm found the optimal values for $\theta$, and is now able to correctly classify all 50 test samples. Had the data not been linearly separable, it would have been a whole other story.
In the next post, we will cover some slightly more complex terrain in order to see how we can get closer to modelling data that is not linearly separable.