How to Build (and Understand) a Neural Network Pt. 4: Backpropagation

In this final post of the series, we will see how to apply backpropagation to the neural net we built in the last chapter. This will allow our network to incrementally improve itself as it gets exposed to new data, which will ultimately enable it to classify the MNIST test set with close to 95% accuracy.

Recall how we optimized our logistic regression model in Pt. 2 by minimizing a loss function using gradient descent? Since backpropagation relies heavily on gradient descent, the intuition behind it bears repeating.

As we saw in Pt. 2, a loss function produces a quantitative measure of the classification accuracy of our model. Given that our model only consists of our weights and biases, it is helpful to imagine a landscape with peaks and valleys (like the one above), where navigating along the $x$ and $y$ axes corresponds to changing our parameters, and where the change in elevation along the $z$ axis corresponds to the resulting change in our loss function. As our model becomes increasingly accurate, the average output of the loss function decreases. When navigating the landscape, this is why we try our best to descend toward the deepest valleys.

Keep in mind that this only serves as a helpful mental image, and not an accurate representation of what is actually going on. In reality, our model will have thousands of parameters, and the peaks and valleys will thus be embedded in very high-dimensional spaces that are impossible to visualize.

The chain rule

As we explored in the previous post, the objective of a learning algorithm for a neural network is to find a configuration of weights and biases that transform the input data into a probability distribution over all of the classes the input sample can belong to.

If we zoom in on what happens to a single sample $a^{(1)}$ as it passes through a network with $l$ layers, we can represent its journey like this:

€€ a^{(2)} = \sigma(\Theta^{(1)}a^{(1)}+b^{(1)}) €€

€€ a^{(3)} = \sigma(\Theta^{(2)}a^{(2)}+b^{(2)}) €€

€€ \vdots €€

€€ \hat{y} = \text{softmax}(\Theta^{(l-1)}a^{(l-1)}+b^{(l-1)}) €€

In order to see exactly how our weights are affecting the loss (and thus how changing them can move us closer to the valleys), we need to brush up on the chain rule. The chain rule tells us how to derive a function with respect to variables inside nested functions. For instance, take the following expression:

€€ f(g(2x)) €€

If we want to know how the value of $x$ influences the value of $f$, the chain rule tells us that we have to derive the outside function and then incrementally multiply by the derivatives of the nested functions like so:

€€ \frac{\partial f}{\partial x} = \frac{\partial f}{\partial g} \cdot \frac{\partial g}{\partial 2x} \cdot \frac{\partial 2x}{\partial x} €€

What this expression signifies is actually quite remarkable. It tells us exactly how changing the value of $x$ affects the value of $f$, even though $x$ is buried inside multiple nested functions. This is crucial knowledge when the time comes to navigate the landscape of the loss function.

A small update to the cross-entropy loss function

This is the cross-entropy loss function. It looks a little different from the one we saw in Pt. 2, but the idea behind it is exactly the same.

€€ \frac{1}{m} \sum\limits_{j=1}^{m} \sum\limits_{i=1}^{n} - y_{i,j} \log(\hat{y}_{i,j}) - (1 - y_{i,j}) \log(1 - \hat{y}_{i,j}) €€

Where in Pt. 2, we only had a single output for each sample, now we have 10 (each output represents the probability of the input image being a digit from 0-9), so instead of merely summing over $m$ samples, we also sum over the $n$ outputs for each sample.

Backpropagating our way through a three-layered network

In the following, we will explore the mechanics of backpropagation through a three-layered neural network (a network with one input layer, one hidden layer, and one output layer) and for a mini-batch $A^{(1)}$ of 75 samples. The entire forward pass of such a network (including evaluation of the cross-entropy loss function $C$) can be expressed like this:

€€ C(\hat{Y}, Y) = C(\text{softmax}(\Theta^{(2)}\sigma(\Theta^{(1)}A^{(1)}+b^{(1)}) + b^{(2)}), Y) €€

With our neural net represented as functions nested inside other functions, we’re now poised to figure out how changing the parameters $\Theta^{(1)}$, $\Theta^{(2)}$, $b^{(1)}$, and $b^{(2)}$ influences the loss $C$. To do this, we first need to find $\frac{\partial C}{\partial b^{(2)}}$ and $\frac{\partial C}{\partial \Theta^{(2)}}$, and this is where the chain rule comes into the picture.

Notice that since our parameters are not represented as scalars but as vectors and matrices, we will be using the gradient notation $\nabla_{\hat{Y}}C$ instead of $\frac{\partial C}{\partial \hat{Y}}$.

When we apply the chain rule to find the gradient of $C$ w.r.t. $b^{(2)}$ and $\Theta^{(2)}$, we get the following:

€€ \nabla_{b^{(2)}}C = \nabla_{Z^{(2)}} \hat{Y} \odot \nabla_{\hat{Y}}C €€

€€ \nabla_{\Theta^{(2)}}C = \nabla_{b^{(2)}}C \times (\nabla_{\Theta^{(2)}}Z^{(2)})^{\text{T}} €€

This expression demands a bit of explanation:

• $\odot$ signifies “element-wise multiplication”. That is, if you have two matrices of equal dimensions, you multiply their corresponding elements, resulting in a new, identically shaped matrix.
• $Z^{(2)}$ is our shorthand expression for the weighted input to the output layer. This would be a $10 \times 1$ matrix given a single sample as input to the network, and a $10 \times 75$ matrix given a mini-batch of 75 samples.
• Superscript $\text{T}$ means transposition. When you transpose a matrix, you turn its row vectors into column vectors and vice-versa. Thus, a transposed $5 \times 10$ matrix is a $10 \times 5$ matrix.

With that out of the way, let us walk through the expression one step at a time: First we do element-wise multiplication between $\nabla_{\hat{Y}}C$ and $\nabla_{Z^{(2)}} \hat{Y}$. Since the shape of both of these matrices is $10 \times 75$, the result is a new $10 \times 75$ matrix containing the products of their corresponding elements. To get the average of ${\nabla_{b^{(2)}}}C$, we collapse it into a $10 \times 1$ vector by summing along all 10 rows. The resulting $10 \times 1$ vector is then divided by 75 in order to give us the average gradient across all 75 samples in the mini-batch.

Given that $\nabla_{\Theta^{(2)}}Z^{(2)}$ contains the partial derivatives w.r.t. each weight in $\Theta^{(2)}$, $\nabla_{\Theta^{(2)}}Z^{(2)}$ must be equal to the activations of the hidden layer $A^{(2)}$. If we assume that the hidden layer has three neurons, $\nabla_{\Theta^{(2)}}Z^{(2)}$ must therefore be of shape $3 \times 75$. Multiplying ${\nabla_{b^{(2)}}}C$ by the transpose of $\nabla_{\Theta^{(2)}}Z^{(2)}$ yields a $10 \times 3$ matrix that matches the shape of $\Theta^{(2)}$. Note that had we not transposed $\nabla_{\Theta^{(2)}}Z^{(2)}$, we wouldn’t have been able to multiply the two matrices, since their original shapes don’t match up.

Matrix multiplication can be quite tricky to wrap one’s head around, so don’t sweat it if you are a bit perplexed. Just know that, had we been dealing with scalars, the equivalent expressions would look like this:

€€ \frac{\partial C}{\partial b^{(2)}} = \frac{\partial C}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z^{(2)}} €€ €€ \frac{\partial C}{\partial \Theta^{(2)}} = \frac{\partial C}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z^{(2)}} \cdot \frac{\partial z^{(2)}}{\partial \Theta^{(2)}} €€

We now have the derivatives of $C$ w.r.t. each individual weight in $\Theta^{(2)}$. However, these are the combined gradients of all 75 samples in our mini-batch. To get some truly useful values, we simply have to divide by 75. This way, we again get the average of our 75 individual gradients, and we will thus minimize the loss function in a way that satisfies the greatest possible number of samples. Neat!

One more thing regarding the above expression: When you do element-wise multiplication between $\nabla_{\hat{Y}}C$ and $\nabla_{Z^{(2)}} \hat{Y}$, you discover something wonderful: It turns out that it simplifies to $\hat{Y}-Y$.

Knowing all of this, the final expression for $\nabla_{\Theta^{(2)}}C$ for a mini-batch of $m$ samples can now be expressed as:

€€ \nabla_{\Theta^{(2)}}C = \frac{1}{m}((\hat{Y}-Y) \times (A^{(2)})^{\text{T}}) €€

Our hypothetical network has one hidden layer, which means it has two sets of weights and biases. We will therefore need to find $\nabla_{\Theta^{(1)}}C$ and $\nabla_{b^{(1)}}C$ as well. Since derivations like these can become quite tedious, I will skip most of them going forward. If you want, you can try and do them yourself — it’s a good exercise!

Once you have found the gradients for all weights and biases, it is time to update their values. In Pt. 2, we updated our parameters using the following update rule:

€€ \Theta^{(i)}:=\Theta^{(i)}-\nabla_{\Theta^{(i)}}C €€

This time, we are going to do almost the same; the slight twist being that I am going to introduce a learning rate. As the name implies, a learning rate (denoted $\alpha$) determines the rate with which our model learns, and is simply a coefficient on the gradient. While a learning rate sounds like something you would want to crank all the way up, this immediately creates a problem.

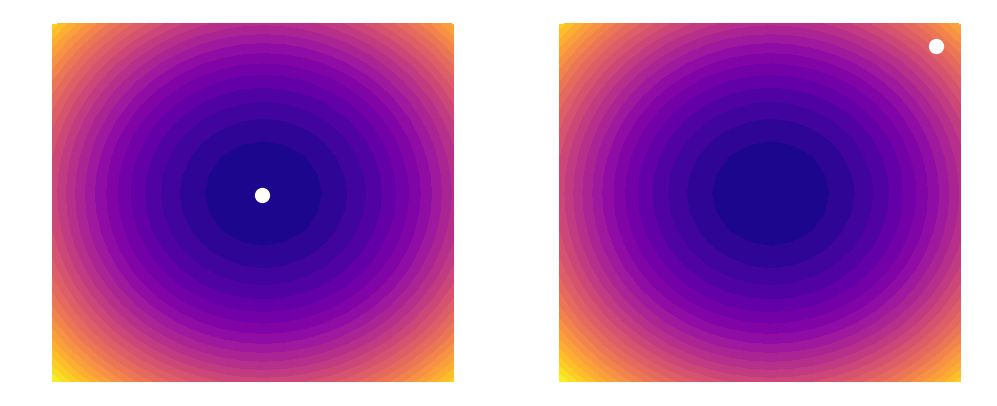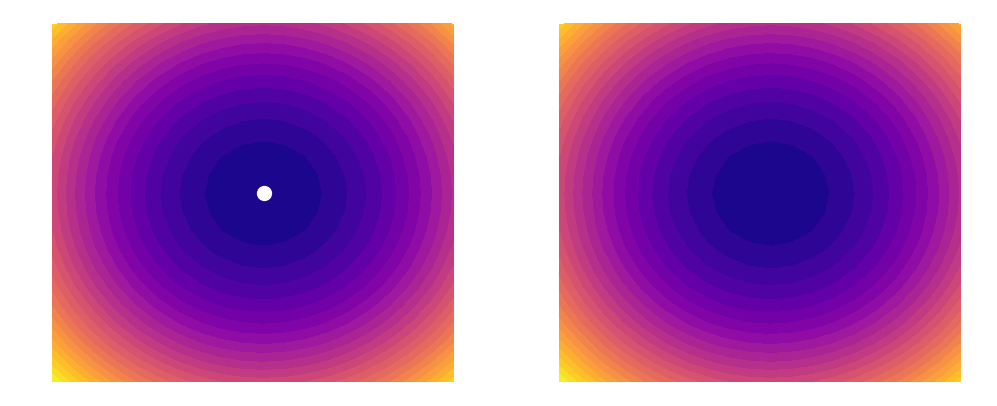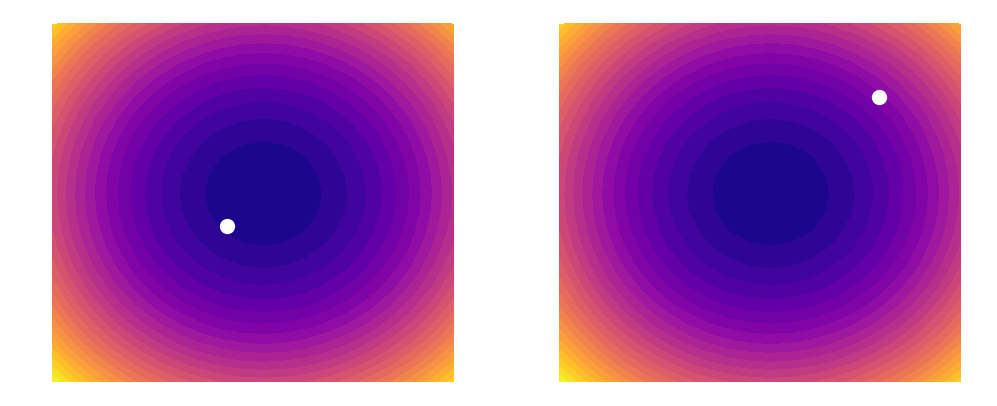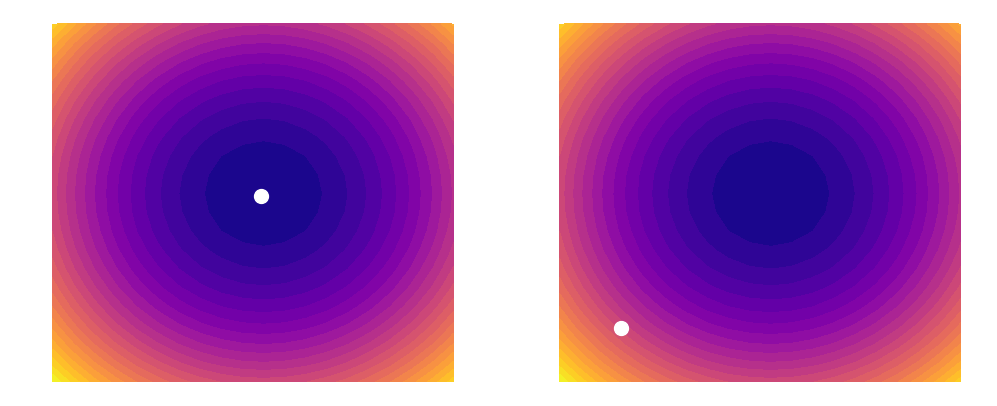
As shown above, a learning rate which is too large (illustrated on the right) can cause an algorithm to overshoot the minimum of its loss function. This happens because increasing the learning rate tells our parameters to take bigger and bigger steps when moving across the landscape. Since the steps are proportional to the slope of the function at any given point, a large learning rate can cause a runaway effect (as shown above). At the same time however, you want the learning rate to be large enough to approach the minimum at as rapid a pace as possible. Finding a good balance can be difficult, which is why techniques such as learning rate decay (that are outside the scope of this post) have been invented. In this example, we will simply be using a constant learning rate of 0.002. Our update rules will thus look like this:

€€ \Theta^{(i)}:=\Theta^{(i)}-0.002 \cdot \nabla_{\Theta^{(i)}}C €€

€€ b^{(i)} := b^{(i)} - 0.002 \cdot \nabla_{b^{(i)}}C €€

Each time we have sent a mini-batch through the network, we calculate the gradient with respect to all of our parameters and use these to update their values. This results in the network being slightly better equipped to classify samples during the next forward pass, since we have inched a little closer to the bottom of a valley.

Backpropagation in code

To apply what we have learned, we will extend our NeuralNetWork class to support backpropagation. To brush up your memory, here is the code we wrote in Pt. 3:

import numpy as np

class NeuralNetwork(object):
    def __init__(self, layer_sizes, alpha=0.1):
        super(NeuralNetwork, self).__init__()

        n_layers = len(layer_sizes)

        if (n_layers >= 3):
            self.thetas = []
            self.biases = []

            for i in range(n_layers-1): # a network with n layers has n-1 set of weights and biases
                self.thetas.append(np.random.randn(layer_sizes[i+1], layer_sizes[i]))
                self.biases.append(np.random.randn(layer_sizes[i+1], 1))

            self.thetas = np.array(self.thetas)
            self.biases = np.array(self.biases)
            self.alpha = alpha
        else:
            raise ValueError("The minimum number of layers is 3 (%i provided)" % n_layers)

    def forward_pass(self, A):
        Zs = []
        As = [A]

        for i in range(len(self.thetas)):
            Z = np.dot(self.thetas[i], As[-1]) + self.biases[i]
            Zs.append(Z)

            if i < len(self.thetas)-1:
                As.append(self.sigmoid(Z))
            else:
                Y_hat = self.softmax(Z)

        return (Zs, As, Y_hat)

    def sigmoid(self, Z): return 1.0 / (1.0 + np.exp(-Z))
    def softmax(self, Z): return np.exp(Z) / np.sum(np.exp(Z), axis=0)

First, we will add a method sigmoid_prime to NeuralNetwork. This will be the derivative of the sigmoid activation function $\frac{\partial \sigma}{\partial z}$.

def sigmoid_prime(self, z): return self.sigmoid(z) * (1 - self.sigmoid(z))

Next, we will add a backprop method to handle gradient derivation:

def backprop(self, Zs, As, Y_hat, Y):
    weight_gradients, bias_gradients = [], []
    bias_gradient = Y_hat - Y

    for i in reversed(range(len(self.thetas))):
        weight_gradients.append(1 / len(Y) * np.dot(bias_gradient, As[i].T))
        bias_gradients.append(1 / len(Y) * np.sum(bias_gradient, axis=1)[:, None])

        if i > 0: bias_gradient = np.dot(self.thetas[i].T, bias_gradient) * self.sigmoid_prime(Zs[i-1])

    return np.array(list(reversed(weight_gradients))), np.array(list(reversed(bias_gradients)))

Let’s run through this method one step at a time.

1. We initialize two lists – weight_gradients and bias_gradients — which we will use to hold the gradient matrices for our weights and biases.
2. We calculate bias_gradient, which initially holds a $10 \times 75$ matrix containing the gradients w.r.t. the output layer’s biases for all 75 samples in our mini-batch.
3. We iterate from the output layer towards the input layer (hence reversed()), deriving the weight gradients at each step of the way (note that .T transposes a numpy matrix). We also update the value of bias_gradient to the gradient w.r.t. the biases in the preceding layer, so we can use this value in the next iteration.
4. Since the gradients have been added in reverse order, we return the numpy representation of the reversed weight_gradients and bias_gradients lists.

From here on out, it’s smooth sailing. We’ll first add an update_params method and a cross_entropy method to calculate the loss:

def update_params(self, weight_gradients, bias_gradients):
    self.weights -= self.alpha * weight_gradients
    self.biases -= self.alpha * bias_gradients

def cross_entropy(self, Y, Y_hat): return 1 / Y_hat.size * np.sum(-Y * np.log(Y_hat) - (1 - Y) * np.log(1 - Y_hat))

We will also add a train and a test method that utilize the methods we have already implemented.

def train(self, X, Y, epochs, batch_size=None):
    if batch_size is None: batch_size = X.shape[1]
    num_iter = int(X.shape[1] / batch_size)

    for i in range(epochs):
        for j in range(num_iter):
            Zs, As, Y_hat = self.forward_pass(X[:, batch_size*j:batch_size*j+batch_size])
            weight_gradients, bias_gradients = self.backprop(Zs, As, Y_hat, Y[:, batch_size*j:batch_size*j+batch_size])
            self.update_params(weight_gradients, bias_gradients)

        print("Cost after Epoch #" + str(i+1) + ": " + str(self.cross_entropy(Y[:, batch_size*j:batch_size*j+batch_size], Y_hat)))

def test(self, X, Y):
    Zs, As, Y_hat = self.forward_pass(X)
    cost = self.cross_entropy(Y, Y_hat)

    num_samples = X.shape[1] # samples are column vectors
    num_wrong = np.count_nonzero(np.argmax(Y_hat, 0) - np.argmax(Y, 0))
    num_right = num_samples - num_wrong
    accuracy = (num_right / num_samples) * 100

    print("Number of correctly classified images: " + str(num_right) + " out of " + str(num_samples) + " (" + str(accuracy) + ")")

Downloading MNIST

To download the MNIST dataset, we will use a Python script called python-mnist that will make it easy for us to fetch and parse the images in a few lines of code.

First, clone the repo to a fitting directory by running the following command:

git clone https://github.com/sorki/python-mnist

To download MNIST, run

cd python-mnist
./get_data.sh

and the dataset should appear as binary files in a new data directory. We will also be using python-mnist to process the data, so for this, you can either reference the files you just cloned, or you can install python-mnist globally using pip:

pip3 install python-mnist

Preprocessing the data

In order to use the dataset, it needs to be in a format that matches the architecture of the network we have built.

To do this, create a new Python file called main.py in the same directory as neural_network.py. In it, import the MNIST class from python-mnist as well as NumPy, pickle and our NeuralNetwork class.

import pickle # for saving the neural net to disk after training
import numpy as np
from mnist import MNIST
from neural_network import NeuralNetwork

Next, let’s load the actual MNIST data into memory. The load_training and load_testing methods in python-mnist will convert the binary files we downloaded before into regular Python lists.

print("Loading MNIST...")
mndata = MNIST('python-mnist/data')
train_images, train_labels = mndata.load_training()
test_images, test_labels = mndata.load_testing()

Since we’ll need the functionality provided by numpy arrays inside of our neural net, we convert the lists train_images and test_images by wrapping them in a call to np.array(). We also need to convert the labels into a proper format.

>>> train_labels[0]
5

As you can see, the labels are represented as a single number between 0-9. You may remember that in order to compute the loss, we need not just the network’s outputted probability distribution, but the ground truth for each of the 10 possible classes as well. Concretely, we want something like this instead:

>>> train_labels[0]
[0, 0, 0, 0, 0, 1, 0, 0, 0, 0]

The code below ensures that the variables X_train, Y_train, X_test, and Y_test contains the samples and labels in a format suited to our network. It also performs feature standardization (see Pt. 2) on the samples to keep the numbers small.

X_train = np.array(train_images, dtype=np.float32)
Y_train = np.zeros((10, len(train_labels)))
X_test = np.array(test_images, dtype=np.float32)
Y_test = np.zeros((10, len(test_labels)))

print("One-hot encoding labels...")
for i in range(len(train_labels)): Y_train[train_labels[i], i] = 1
for i in range(len(test_labels)): Y_test[test_labels[i], i] = 1

print("Performing feature standardization...")
for i in range(len(X_train)): X_train[i] = (X_train[i] - np.mean(X_train[i])) / np.std(X_train[i])
for i in range(len(X_test)): X_test[i] = (X_test[i] - np.mean(X_test[i])) / np.std(X_test[i])

Training and testing our network

The time has now finally come to initialize our neural network. I have chosen an architecture of six hidden layers each containing 50 neurons, and a learning rate of 0.002:

nn = NeuralNetwork(layer_sizes=[784,50,50,50,50,50,50,10], alpha=0.002)

As you can see, we have made it easy to tweak and tune the hyperparameters of the network, so feel free to experiment as much as you’d like.

We can now train the network by calling the train method, then test its accuracy by calling test immediately afterwards. We will also make sure to save it to disk using pickle in case you want to mess around with it afterwards. Note that the X_train and X_test are transposed, since we want each sample to be represented by a column vector.

print("Beginning training...")
nn = NeuralNetwork(layer_sizes=[784,50,50,50,50,50,50,10], alpha=0.002)
nn.train(X_train.T, Y_train, epochs=1500, batch_size=10)

print("Testing...")
nn.test(X_test.T, Y_test)

print("Saving the neural net to disk...")
pickle.dump(nn, open("neural_net.p", "wb"))

print("Done")

With these settings, we are going to feed all the images to the network in batches of 10, and we will do that a thousand times. Since there are 60,000 images in the training set, this means that our network has to crunch through 60,000,000 images and update its 52,510 parameters 6,000,000 times. It goes without saying that this is quite an intensive and time-consuming operation, so expect a training time of a couple of hours.

Once you run the script, you should see something similar to the output below. Note that the values aren’t going to be identical, since the parameters of the network have been randomly initialized. The important thing is that the loss is decreasing.

loss after Epoch #1: 0.323842013643
loss after Epoch #2: 0.287431827718
loss after Epoch #3: 0.273531054997
loss after Epoch #4: 0.268344457733
loss after Epoch #5: 0.243978653084

By the end of the 1000 epochs, the network’s accuracy on the test set will be printed out:

Number of correctly classified images: 9364 of 10000 (0.9364% accuracy)

Conclusion

Congratulations! If you have made it all the way through these four parts, I hope you now have a much better understanding of neural nets and how they work. It goes without saying that there is still tons more to learn; even about vanilla neural nets like the ones we have been working with. These include learning rate decay, regularization, alternative activation functions, and much more!

In future posts, I intend to build upon the basic knowledge we have acquired in this series to explore other exciting machine learning methods, such as GANs, capsule networks, and various NLP techniques. Stay tuned, and thanks a lot for reading!