The Inner Workings of Convolutional Nets

Of all the stunning advancements in deep learning made in the last 10 years, the progress in the field of computer vision is perhaps the most striking. At the heart of this progress is a model known as a convolutional neural network – or “CNN” for short – which resembles the structure of the brain’s visual cortex and has become a staple of almost all computer vision systems today.

In this post, we will begin by exploring the structure and operations of convolutional nets including kernels, stride, zero-padding, pooling, and more. We will also look at simple regularization techniques that improve a model’s generalization. Finally, we will create and train our own CNN using Keras on an image set known as CIFAR-10, achieving around 85% accuracy.

CIFAR-10

The CIFAR-10 dataset contains 60,000 $32 \times 32$ images, 50,000 of which are training images. Each image belongs to one of the following 10 classes:

All classes are mutually exclusive and are allotted an equal number of images.

What is a convolutional net?

If you followed my series on How to Build (and Understand) a Neural Network, you will remember that a “fully connected” or “dense” neural network takes as input one or more data samples, each represented by a flat $n$-dimensional vector. While this is fine for relatively simple problems like MNIST, the one-dimensional structure of the input presents a serious limitation to the kinds of patterns a dense network can discover in the data.

For instance, take a moment to consider the problem of object detection in images using a dense neural network. In order to distinguish between objects – say an apple and a banana – a network needs to incorporate some sort of “shape detection” from which it can draw its distinction. But given the flatness of its input, a dense network has no concept of vertical versus horizontal, and it would thus be blind to a crucial property of its input; namely its multidimensionality.

Flattened $8 \times 8$ images of a banana, apple, orange, kiwi, and pear. This is what a dense network sees.

This is where convolutional neural nets come into the picture (no pun intended). A CNN is a specialized type of neural network that vastly outperforms dense networks in image recognition tasks, and they do this by first preserving the dimensionality of their input.

Unflattened $8 \times 8$ images of a banana, apple, orange, kiwi, and pear. This is what a convolutional neural network sees.

Another key property of CNNs, and the one responsible for their name, is the use of convolutions in place of regular matrix multiplications. Let’s see what this means.

Recall that a dense network has full connectivity, meaning that all of its hidden neurons are dependent on all neurons in the preceding layer. What convolution does is it introduces sparse connectivity, meaning that each hidden neuron is now only dependent on a fixed subset of the neurons in the preceding layer. The difference can be seen in the following illustration.

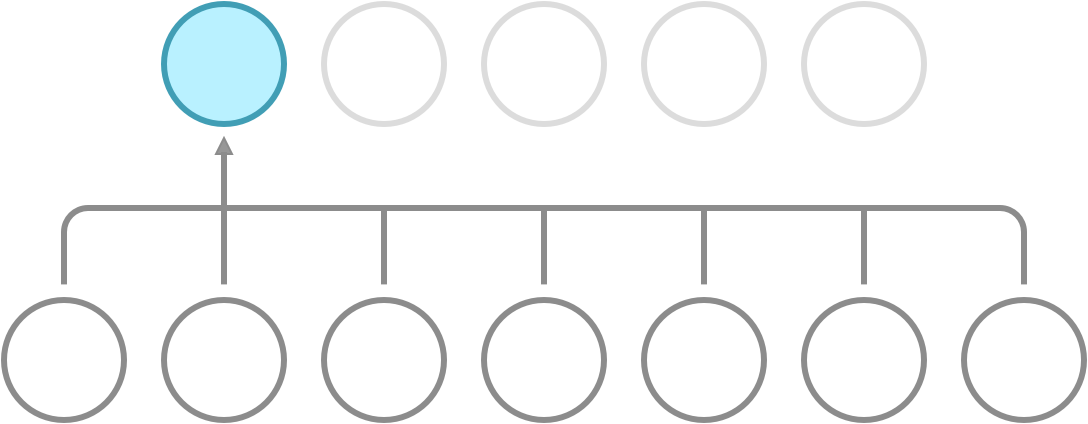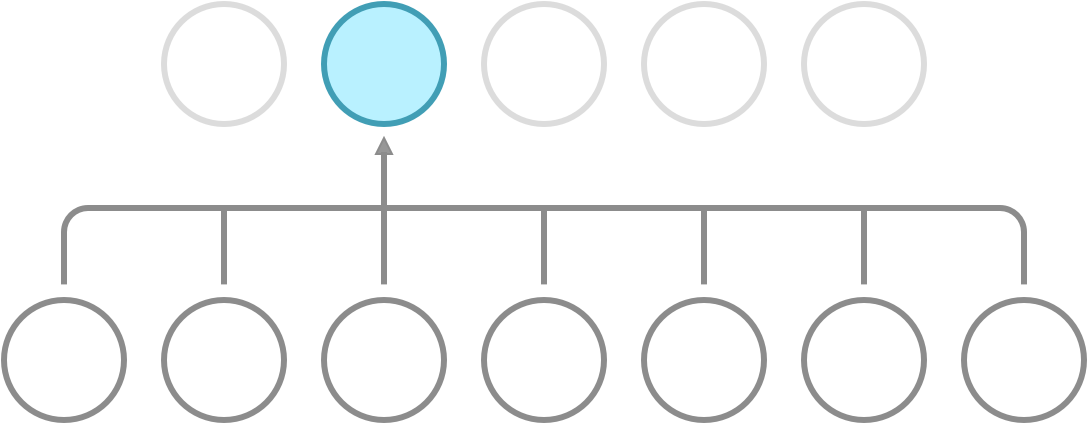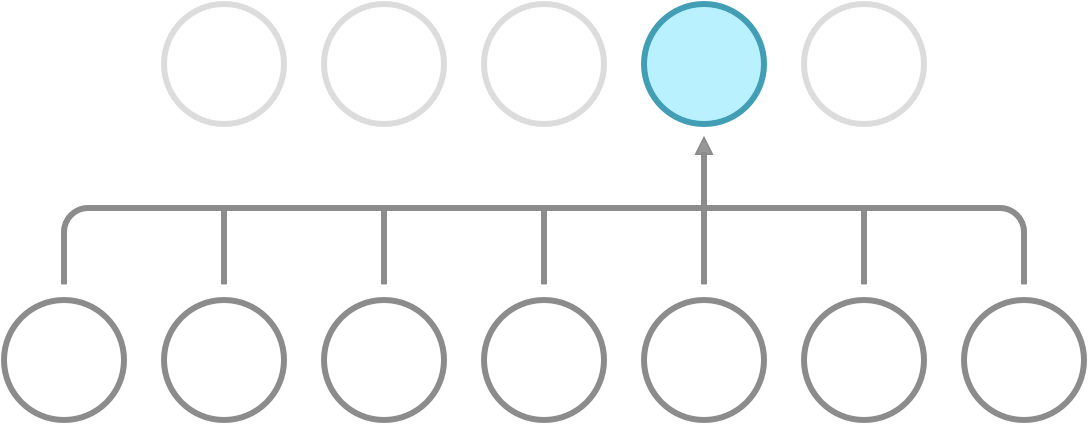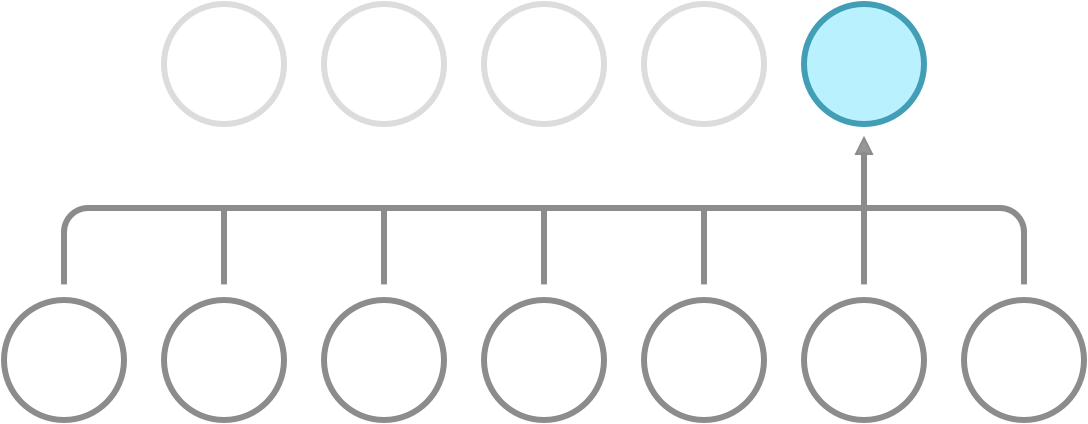
Full connectivity. Each neuron receives input from all neurons in the preceding layer.

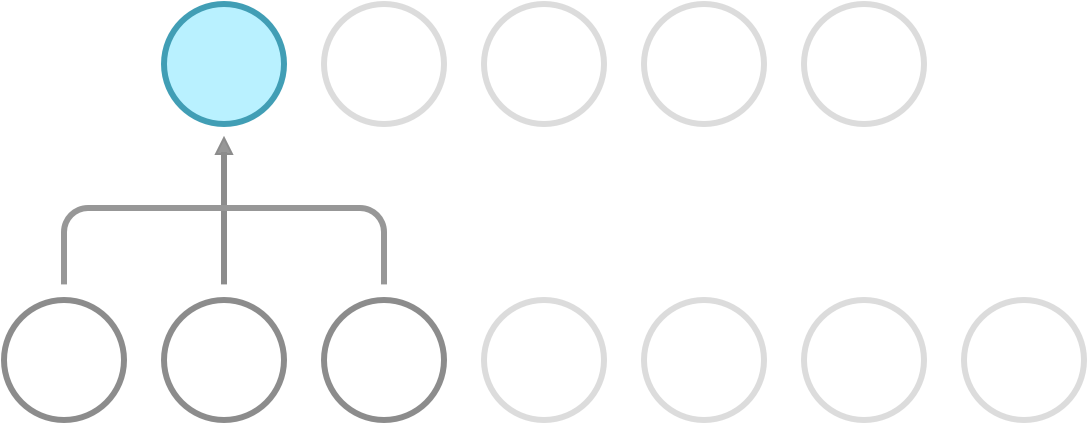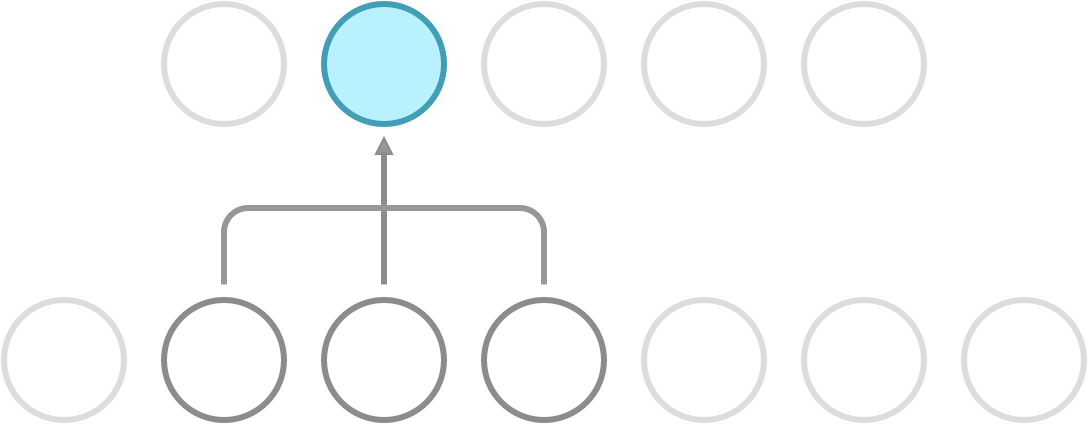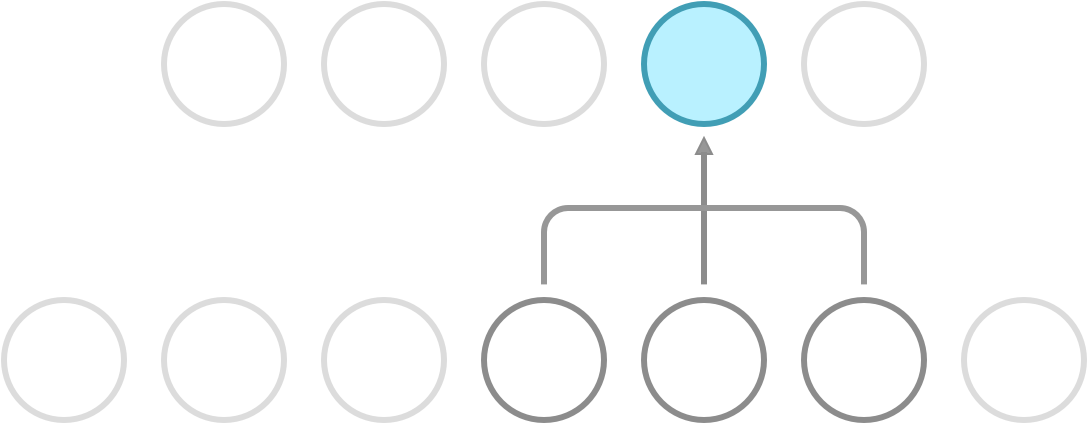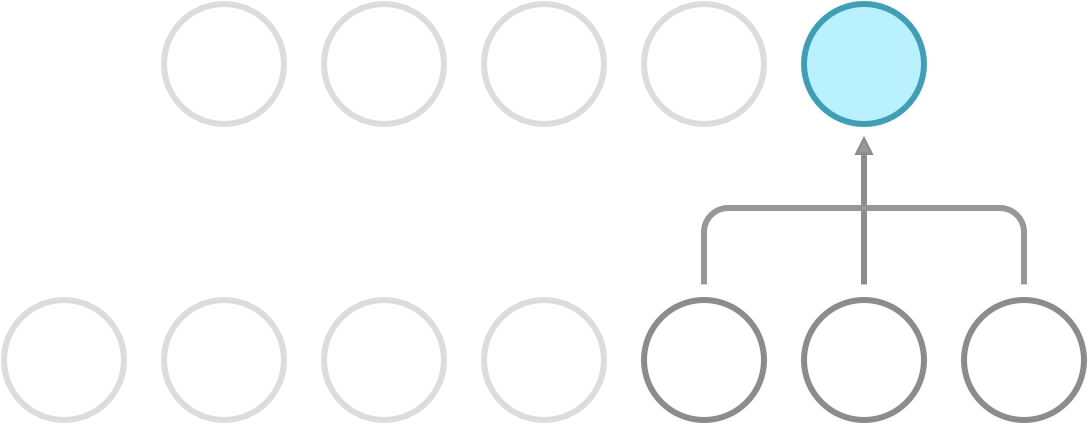
Sparse connectivity. Each neuron receives input from a fixed subset of neurons in the preceding layer.

In a dense network, the weight between a pair of input and output neurons is never shared with another pair of input and output neurons. In a CNN, this is not so. Here, you use a fixed set of weights called a kernel, and slide it over the entire input. This property is called weight sharing, and is one of the primary reasons that CNNs outperform dense networks in accuracy as well as memory efficiency.

To illustrate how the use of sparse connectivity and weight sharing reduces memory consumption compared to a dense network working on the same data, assume we used a dense network to process RGB images of size $512 \times 512$ pixels. A single image would then be represented by a $512 \times 512 \times 3$ matrix, which, when flattened, would produce a vector of dimension $786.432$. Assuming the first hidden layer in our network had 100 neurons, the first weight matrix alone would have $786.432 \times 100 = 78.643.200$ elements!

Conversely, a convolutional net operating on the same flattened data and with 100 units of output after its first convolution would only require $786.333$ individual weights between the first and second layer (a reduction of 100x). This is because the size of the output equals $m - k + 1$ where $m$ is the size of the input and $k$ is the size of the kernel. Can you see why by looking at the illustration above?

Kernels

So far, we have talked about the properties of convolutional networks in the context of flat data. Exploring how they operate on higher dimensional data will no doubt make things a bit more interesting. To do that, let us first try to visualize the operations of a CNN with a $3 \times 3$ kernel on a downsampled $8 \times 8$ image from the CIFAR-10 dataset.

There are a few things to bear in mind here. First, while the illustration shows the image as a two-dimensional structure, it is in fact three-dimensional given that it has a width, a height, and a depth in the form of an RGB channel. This means that the kernel itself is actually a $3 \times 3 \times 3$ matrix. Each distinct output – illustrated by the gray and black pixels – is computed in the following way:

The $3 \times 3 \times 3$ kernel is multiplied element-wise with whatever $3 \times 3 \times 3$ region of the input is below it (sometimes called the receptive field). The result of this operation is a new matrix of the same shape, and the sum of all the elements in this matrix is the output at one particular location. This means that, as opposed to the input and the kernel, the output of a convolution is always two-dimensional (hence my attempt to illustrate the output using grayscale colors).

More formally, the scalar output $z$ at one location is the sum of all elements in the entrywise product of the current receptive field $R$ and the kernel $K$:

€€ H = R \odot K €€

Entrywise or “Hadamard” product of the kernel and receptive field.

€€ z = \sum_{l=1}^d \sum_{i=1}^{k} \sum_{j=1}^{k} h_{i,j,l} €€

Sum of all elements in the entrywise product. $k$ is the width and height of the kernel and receptive field, while $d$ is the depth.

A second thing to notice is how the use of weight sharing produces the sense of the kernel sliding over the image. The discrete applications of the same kernel across the entire input results in an important and characteristic property of convolutional nets called translational invariance.

Translational invariance means that whatever pattern a kernel has been trained to recognize – be it horizontal lines or the round shape of an apple – this information will be embedded in the activation regardless of where in the input the pattern appears.

As we will see in the next post on feature visualization, the patterns that are picked up by kernels in the initial layers of a convolutional net usually pertain to the simplest components of the visual world, such as horizontal or vertical lines. As one proceeds through the layers however, the patterns become gradually more complex, such as the shape of eyes and ears, and ultimately the overall characteristics of a person’s face (insofar as the model has been trained to perform facial recognition of course).

With kernels acting as the pattern-finding components of convolutional nets, multiple kernels are always needed to solve any kind of complex problem. The illustration below shows three distinct convolutions by three distinct kernels, as well as how the outputs of each are combined to produce a cohesive whole. Again, it is important to emphasize that the depth of a kernel always equals the depth of the input while the width and height are usually much smaller.

If there are $n$ kernels of size $k \times k \times d$, the output produced by convolving over an input of size $m \times m \times d$ will be $(m - k + 1) \times (m - k + 1) \times n$. In the above case, this comes out to $6 \times 6 \times 3$, which, in this particular example, can be roughly interpreted as a $6 \times 6$ RGB image. This image would then be fed as input to the subsequent convolutional layer in the network.

Stride

Another hyperparameter, aside from the size and number of kernels, is stride. In the illustrations shown so far, we have used a stride of $1$, meaning that the kernels sweep across the image in steps of one pixel at a time. To decrease – or even eliminate – the overlap of receptive fields that results from this, we can increase the stride, and force the kernel to take bigger steps along the $x$ and $y$ axes of the input. With stride now in the picture, we need to update the formula for the output size $z$ to:

€€ z = \frac{m - k}{s} + 1 €€

Where $s=\text{stride}$.

One thing to notice is that increasing the stride always decreases the size of the output along the width and height dimensions. This sometimes proves practical in situations where we want to downscale the computational burden on subsequent layers.

Zero-padding

One problem we are currently facing is that a convolution with a kernel larger than $1 \times 1$ always produces an output smaller than the input. The reason why this is a problem is that it puts an upper bound on the number of layers we can have in our network. To solve this, we use zero-padding, which is simply making the input volume bigger by padding it with zeros along the borders.

The final formula for the output size thus becomes:

€€ z = \frac{(m + 2p) - k}{s} + 1 €€

Where $p=\text{zero-padding}$.

Now, as long as we know the size of the input $m$ and kernel $k$ as well as the stride $s$, we can always rearrange the above expression to find a $p$ which produces an output of the desired size $z$.

It is important to note that since the input can only be padded with a whole number of pixels, $p$ must always be an integer. Naturally, this restriction also holds for stride and kernel size.

ReLU

Just like in a dense network, once a $z \times z \times n$ output matrix has been computed, each element of the matrix is passed – element wise – through a nonlinear activation function.

In the previous series of posts, we used the sigmoid function as our activation function. This time, we will instead use the ReLU function, which is even simpler, and has been shown to work better than its s-shaped counterpart for a wide range of deep learning tasks.

€€ f(x) = \max(x, 0) €€

Pooling

At this point, we have touched on two of the three main components of a convolutional network layer: the convolution itself (with all its associated hyperparameters) and the activation function. The third component, pooling, simplifies the output for the subsequent layer in the network by reducing it to a kind of summary of the actual activations. This step is not strictly necessary, but it is very commonly applied, since it reduces computational load and improves accuracy.

There are multiple variations of pooling; the most common being max pooling, which reduces the size of the input by accentuating the strong activations and attenuating the weaker ones. Similar to sliding a kernel over an image, max pooling takes as input a volume of size $m \times m \times n$ and produces an output of size $\frac{m - k}{s} + 1 \times \frac{m - k}{s} + 1 \times n$ where $k$ is the size of the pooling window and $s$ is the stride. Unlike a kernel however, the pooling window is not a matrix, but simply the region of the input used in each pooling step. This step is very simple: For a window size of $2 \times 2$, output the largest number in the $2 \times 2$ receptive field and discard the others. Note that the pooling window is two-dimensional, and is distinctly applied at each depth layer, meaning that the pooling layer always preserves dimensionality.

Classification

At this point, you might be wondering how we move from convolutional layers to classification. After all, classification ultimately involves a flat vector of probabilities calculated by taking into account the entire input. This is something sparse connectivity doesn’t provide. You could technically use $n=\text{number of classes}$ kernels of the same size as the input and run the results through softmax. But why not just flatten the output of the last convolutional layer, and then use that as input to a simple dense network whose output layer provides us with our classification? (Backpropagation will still work great; we simply push the gradients through to the convolutional network instead of stopping at the dense network’s input layer.)

This architecture is a staple of most CNNs, and for good reason. The convolutional layers are responsible for feature detection, while the dense layers are tasked with discovering which activations correspond to which classes; a decidedly simpler but equally important task.

Implementing a CNN using Keras

Now that we have a basic grasp of much of the underlying theory, let us try to implement our own convolutional network using Keras; an API which acts as a wrapper around Tensorflow, CNTK or Theano. We will be using the Tensorflow version, so everything we need can be installed by running:

pip3 install tensorflow

Once Tensorflow is installed, fetching the CIFAR-10 dataset and configuring, training, testing, and saving our convolutional net is incredibly easy (all the code can be accessed here). Let’s start with the basic setup:

from tensorflow import keras
from tensorflow.keras.datasets import cifar10
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Conv2D, MaxPooling2D, Flatten, Dense, Activation, BatchNormalization
from tensorflow.keras.preprocessing.image import ImageDataGenerator
import numpy as np

# Hyperparameters
NUM_CLASSES = 10
ACTIVATION = "relu"
LEARNING_RATE = 1e-3
BATCH_SIZE = 64
EPOCHS = 64
LOSS_FUNCTION = "categorical_crossentropy"
LAMBDA = 1e-4
REGULARIZER = keras.regularizers.l2(LAMBDA)

# Loading CIFAR-10
(x_train, y_train), (x_test, y_test) = cifar10.load_data()

# Normalizing training samples
mean_train = np.mean(x_train)
std_train = np.std(x_train)
x_train = (x_train - mean_train) / std_train

# Normalizing test samples
mean_test = np.mean(x_test)
std_test = np.std(x_test)
x_test = (x_test - mean_test) / std_test

# One-hot encoding training and testing labels
y_train = keras.utils.to_categorical(y_train, NUM_CLASSES)
y_test  = keras.utils.to_categorical(y_test, NUM_CLASSES)

After importing all the relevant parts of the Keras library, we start by defining our hyperparameters and loading the CIFAR-10 dataset by calling load_data() on the cifar10 module. This will proceed to fetch and load into memory the entire dataset. Afterwards, we normalize all samples, and ensure that the associated labels are one-hot encoded (this is required for computing the network’s loss function).

We can now proceed to set up the model architecture:

# Model architecture
model = Sequential()

model.add(Conv2D(32, (3,3), padding='same', kernel_regularizer=REGULARIZER, input_shape=x_train.shape[1:]))
model.add(Activation(ACTIVATION))
model.add(BatchNormalization())

model.add(Conv2D(32, (3,3), padding='same', kernel_regularizer=REGULARIZER))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Activation(ACTIVATION))
model.add(BatchNormalization())

model.add(Conv2D(64, (3,3), padding='same', kernel_regularizer=REGULARIZER))
model.add(Activation(ACTIVATION))
model.add(BatchNormalization())

model.add(Conv2D(64, (3,3), padding='same', kernel_regularizer=REGULARIZER))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Activation(ACTIVATION))
model.add(BatchNormalization())

model.add(Conv2D(128, (3,3), padding='same', kernel_regularizer=REGULARIZER))
model.add(Activation(ACTIVATION))
model.add(BatchNormalization())

model.add(Conv2D(128, (3,3), padding='same', kernel_regularizer=REGULARIZER))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Activation(ACTIVATION))
model.add(BatchNormalization())

model.add(Flatten())

model.add(Dense(32, activation=ACTIVATION))
model.add(Dense(NUM_CLASSES, activation='softmax'))

model.summary() # Print out a summary

Take a moment to appreciate the simplicity and expressiveness of the Keras API. If you have read everything up until this point, most of the above code should be pretty self-explanatory; perhaps except for batch normalization and kernel regularization.

Batch normalization simply refers to normalizing the activations of a layer, such that it has a mean of 0 and a standard deviation of 1. While this increases the number of operations performed by the network (and thus slows down the forward and backward passes), it actually speeds up learning and results in an overall decrease in convergence time. You can read more about the advantages of batch normalization here.

Kernel regularization refers to adding the individual weights of a kernel to a network’s loss function. This is a very common regularization technique, which prevents overfitting when configured appropriately. If we let $l$ be the value of a loss function for a particular mini batch with no kernel regularization, the value of the loss function with kernel regularization would then be

€€ l + \lambda \sum_{w \in W} w^2 €€

where $W$ equals all weights in all kernels with L2 regularization enabled. The $\lambda$ coefficient determines the power of the regularization. Tune it up enough and your model will surely end up underfitting; tune it down and it will be prone to overfitting. In this case, $\lambda = 0.0001$, which seems to work pretty well. (As you can probably tell, configuring these parameters is not a hard science, and one often has to try out different values to see what works best in a given situation.)

Data augmentation in Keras

In machine learning, one can never take too many measures to boost generalization. Regularization is one such measure, since reducing overfitting implies better generalization. Another simple yet effective technique is data augmentation. This consists of simply taking whatever samples you already have and modifying them in ways (such as by rotation) that subtly change their appearance. A picture of a dog rotated at a 12 degree angle is, after all, still a picture of a dog. Keras has a built-in mechanism for data augmentation, which we set up in the following way:

datagen = ImageDataGenerator(rotation_range=45,
                             width_shift_range=0.1,
                             height_shift_range=0.1,
                             horizontal_flip=True)

This specifies that we will permit rotations between -45 and 45 degrees, horizontal and vertical offsets by less than or equal to 10% of the image’s width/height, and horizontal flips/mirroring.

Training

The time has come to train our model. To do that, we will use the Adam optimizer, which is a more sophisticated variation of stochastic gradient descent. If you are interested, you can read more about it here.

# Training
adam = keras.optimizers.Adam(lr=LEARNING_RATE)
model.compile(loss=LOSS_FUNCTION, optimizer=adam, metrics=['accuracy'])
model.fit_generator(augmented_data, epochs=EPOCHS, verbose=1, validation_data=(x_test, y_test))

# Saving the model to disk
model_json = model.to_json()
with open('model.json', 'w') as json_file:
    json_file.write(model_json)
model.save_weights('model.h5')

Crunching through all 64 epochs will most likely take a couple of hours depending on your hardware. By the 64th epoch, though, you should see an accuracy of about 85% on the test set. To improve this further, I suggest you take a look at this blog post, which outlines how to utilize techniques like learning rate decay and dropout to achieve close to 90% accuracy.

In the next post, we will use the DeepDream feature visualization technique to probe the internals of our own trained CNN as well as more complex pretrained models.